�c���ڿƌW(xu��)�Һ͔�(sh��)�W(xu��)��ʹ�õą���(sh��)��������ȣ��ߵϵđҒ�ģ�͵Ą�(chu��ng)���P(gu��n)�I�ǣ����܉��Ԅ�(d��ng)��Ӌ(j��)����䅢��(sh��)�����̵ĽY(ji��)�����ߵϿ���ͨ�^������(du��)�K�������ã��p�ث@�Ñ�朾����Π�������ֹ���Ӌ(j��)���朾��ą���(sh��)���̡��@�Nģ�MӋ(j��)�㷽����Frei Otto���l(f��)չ������Դ�Է�����Ĥ�ĘOС�����ͨ�^����Һ�w�е���ë���ɵ���С·����
Otto��1996��ʹ�����@Щ����ģ���M(j��n)�����O(sh��)Ӌ(j��)��һ�Nͨ�^̽����Ȼ�ą���(sh��)����ģ��ʽ���ڸߵϵ��(xi��ng)Ŀ�У����ģ���ڷ��������ε�ͬ�r(sh��)Ҳʹ�����O(sh��)Ӌ(j��)���нY(ji��)��(g��u)���������w�����Ү�(d��ng)�ߵ��{(di��o)��ģ�͵ą���(sh��)�r(sh��)��ģ�͵��ΑB(t��i)Ҳ��(hu��)�Ԅ�(d��ng)�İl(f��)����׃���@�M���˅���(sh��)����ģ���x�dz���Ҫ��һ���֣�������(sh��)����ģ�ă�(y��u)�c(di��n)������̽���ĽY(ji��)���Ļ��A(ch��)�ϡ������(du��)�څ���(sh��)���Ķ��x���]�и�׃���@Щͨ�^ģ�M����(sh��)�F(xi��n)�ą���(sh��)��ģ�ͣ�������һϵ�е�ͨ�^��(d��)���ą���(sh��)�c�@����(sh��)�\(y��n)����õ�������Ȼ���@�������ڌ�(du��)ģ���ṩ�Ŀ����Ե�̽��֮�ϡ�

����ķ��ܴ�d���, 1970-1975��, ������ķ ��Frei Otto

(li��n)��@ˇ���[��(hu��)�����^, 1955��, �� ��������Frei Otto
Frei Otto Tips��
Frei Otto ���x�����N��ͬ�Ļ�����ʽ��
1. Direct path networks,
2. Minimal path networks,
3. Minimizing detour networks��
1. Direct path networks, ���B������Ŀ�ĵص��c(di��n)���@����ֱ�ӣ�Ҳ��M(f��i)�X�ӵ�·�����D��Rhino���傀(g��)�c(di��n)ȫ���B�ӵ�һ��(g��) Direct path networks.
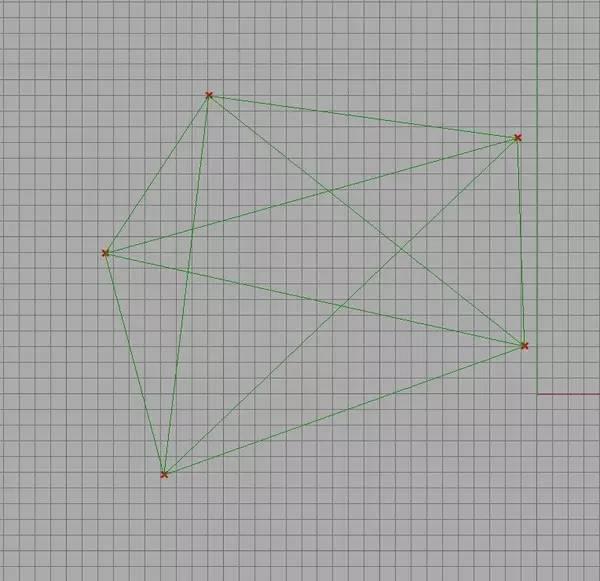
ֱ��·���D��
2����(du��)��Minimal path networks���о���FreiOtto�ٴ�ʹ���˚���ﵣ����������|(zh��)������ԣ����о�ģ�M��Ȼ�l���������ڵ��(ji��)�s�����ķ�(w��n)�B(t��i)���@����ʹ�õĵ����Ƿ�����
�D�Ƿ�����ģ�M��Minimalpath system�����^�����·�������ǃ�(y��u)��֮������о��ε��L����̡��D���б��^��ԭ�����c(di��n)֮�g��Direct path�L�Ȟ�2���������÷�����ԭ���õ���120���A��·�����L�Ȟ�1.93����(sh��)�F(xi��n)��·���L�ȵă�(y��u)����minimal path system, ���˼�x��ͨ�^�@��(g��)��(y��n)��Ĕ�(sh��)�W(xu��)��ʽ�õ�����K�Y(ji��)����·�����L��Ψһ��һ��(g��)��ֵ��Ҳ������Փ�ϵ���Сֵ���@��(g��)ģ����K��һ��(g��)���ģ�ͣ��]���κ�������B�ӡ�
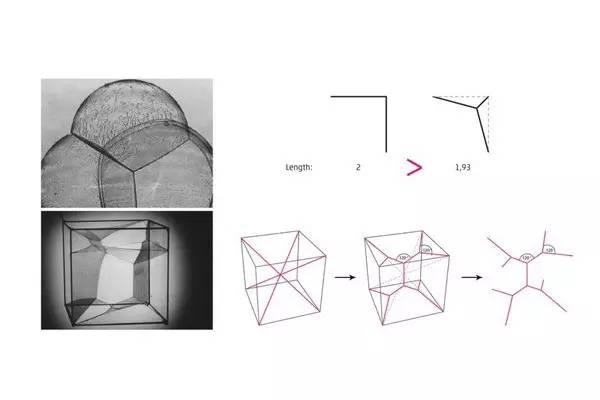
���·���D��
3��������(g��)������ʽDetour path networks�г��F(xi��n)��FreiOtto��һ��(g��)�dz�������ģ�M��(sh��)�(y��n)���ǵģ������õ����ˣ��@���õ�������ë��ģ�� Wool-thread model. ��D���B�Ӹ���(g��)Ŀ���c(di��n)�ĸ������ë���҈D�����ë������ë�˴�֮�g��?y��n)�ˮ�ď���������������һ���γ��˶���(g��)·��׃?y��u)�һ��(g��)·�����D(zhu��n)׃���@��(g��)��(sh��)�(y��n)����D���ڜp�ٸ���(g��)Ŀ���c(di��n)��Direct path�Ŀ��L�ȣ�ͬ�r(sh��)�@Ȧ���ؾS����һ��(g��)���^�͵ķ�����3.Detour path networks �� 2. Minimal path networks �кܶ������c(di��n)�����Ǟ��˿s��·������ͬ̎���ڣ�����2���A������һ��(g��)�����Ĕ�(sh��)�W(xu��)˼·��ģ�M���õ�����Ψһ�⡣��ǰ��3�õ���ģ�M�Y(ji��)��������Ψһ�ģ���?y��n)��T��Ӱ����صIJ�ͬ������K��(hu��)�õ���ͬ�ĽY(ji��)���������@Щ�Y(ji��)���Ĺ�ͬĿ��(bi��o)���ǃ�(y��u)��·�����L�ȡ�
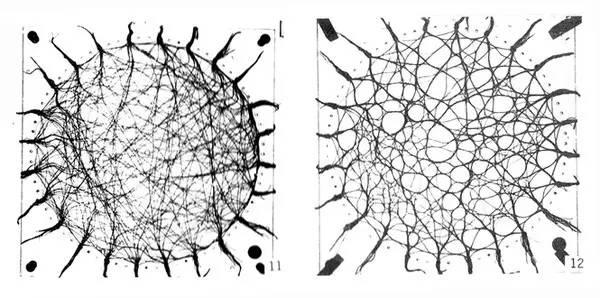
��ë��������ʾ��
��(du��)��Detour path system������Ҳ�Ƿdz��V������?y��n)��ڽ����ИI(y��)�У��O(sh��)Ӌ(j��)������Ψһ�⣬�����f�������O(sh��)Ӌ(j��)���^��(du��)����(hu��)��Ҫ���f�@Ƭ�����ĵ�·���Lһ��Ҫ�M��Minimal path����Փ��Сֵ���෴��һ��(g��)�ж���(g��)�ɿ���(sh��)�����{(di��o)���ֿɃ�(y��u)��·�W(w��ng)���L�ȵ�ģ�M���߲��Ǹ��ã�Detour path system �M�ճ���������Zahahadid��(w��)��2006������˹̹���������@��(g��)�����O(sh��)Ӌ(j��)�������ҕ�lժ����پW(w��ng)��ģ�M����Ώ�Directpath����(y��u)����ĵ�·���D���Π�ĝu׃�^�̣���������(d��ng)��
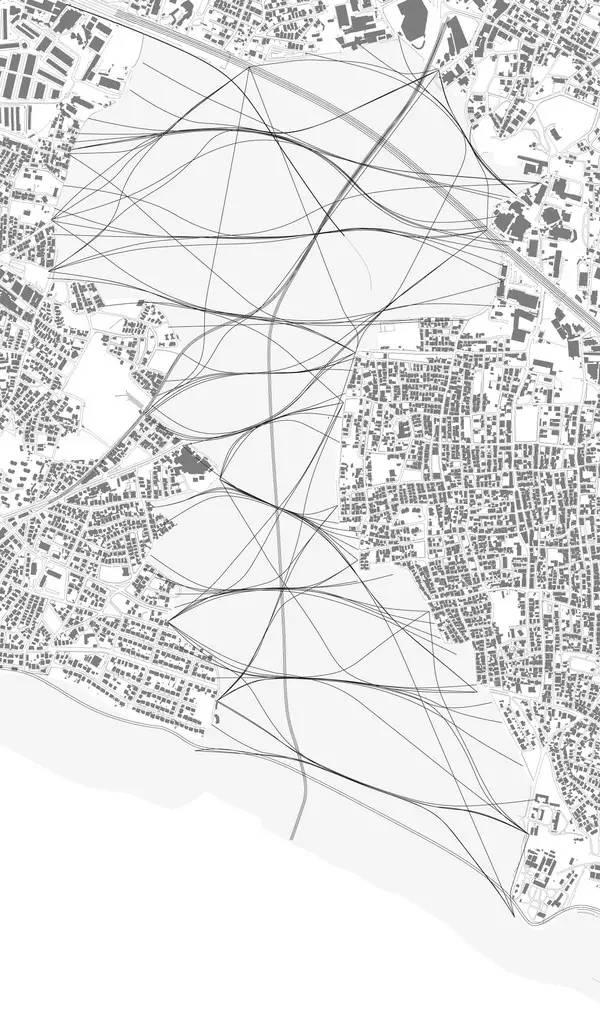
Zaha Hadid ʹ��Detour path system�M(j��n)����˹̹���������O(sh��)Ӌ(j��)
���·��g������Daniel Davis ��A History of Parametric��
���곽 ͬ��(j��)��W(xu��)�����c����Ҏ(gu��)���W(xu��)Ժ�Tʿ�о���



